Variational inference of zQTL regression

fit.zqtl(effect, effect.se, X)

Arguments

effect: Marginal effect size matrix (SNP x trait)
effect.se: Marginal effect size standard error matrix (SNP x trait)
X: Design matrix (reference Ind x SNP)
n: sample size of actual data (will ignore if n = 0)
A: Annotation matrix (SNP x annotations; default: NULL)
multi.C: multivariate SNP confounding factors (SNP x confounder; default: NULL)
univar.C: univariate SNP confounding factors (SNP x confounder; default: NULL)
factored: Fit factored QTL model (default: FALSE)
options: A list of inference/optimization options.
do.hyper: Hyper parameter tuning (default: FALSE)
do.rescale: Rescale z-scores by standard deviation (default: FALSE)
tau: Fixed value of tau
pi: Fixed value of pi
tau.lb: Lower-bound of tau (default: -10)
tau.ub: Upper-bound of tau (default: -4)
pi.lb: Lower-bound of pi (default: -4)
pi.ub: Upper-bound of pi (default: -1)
tol: Convergence criterion (default: 1e-4)
gammax: Maximum precision (default: 1000)
rate: Update rate (default: 1e-2)
decay: Update rate decay (default: 0)
jitter: SD of random jitter for mediation & factorization (default: 0.1)
nsample: Number of stochastic samples (default: 10)
vbiter: Number of variational Bayes iterations (default: 2000)
verbose: Verbosity (default: TRUE)
k: Rank of the factored model (default: 1)
svd.init: initialize by SVD (default: TRUE)
right.nn: non-negativity in factored effect (default: FALSE)
mu.min: mininum non-negativity weight (default: 0.01)
print.interv: Printing interval (default: 10)
nthread: Number of threads during calculation (default: 1)
eigen.tol: Error tolerance in Eigen decomposition (default: 0.01)
eigen.reg: Regularization of Eigen decomposition (default: 0.0)
do.stdize: Standardize (default: TRUE)
out.residual: estimate residual z-scores (default: FALSE)
do.var.calc: variance calculation (default: FALSE)
nboot: Number of bootstraps (default: 0)
nboot.var: Number of bootstraps for variance estimation (default: 100)
scale.var: Scaled variance calculation (default: FALSE)
min.se: Minimum level of SE (default: 1e-4)
rseed: Random seed

Value

a list of variational inference results.

param: sparse genetic effect size (theta, theta.var, lodds)
param.left: the left factor for the factored effect
param.right: the left factor for the factored effect
conf.multi: association with multivariate confounding variables
conf.uni: association with univariate confounding variables
resid: residuals
gwas.clean: cleansed version of univariate GWAS effects
var: variance decomposition results
llik: log-likelihood trace over the optimization

Details

Estimate true effect matrix from marginal effect sizes and standard errors (Hormozdiari et al., 2015; Zhu and Stephens, 2016): $$\mathbf{Z}_{t} \sim \mathcal{N}\!\left(R E^{-1} \boldsymbol{\theta}_{t}, R\right)$$ where R is $p \times p$ LD / covariance matrix; E is expected squared effect size matrix ($\textsf{se}[\boldsymbol{\theta}_{t}^{\textsf{marg}}] + n^{-1} \langle \boldsymbol{\theta}_{t}^{\textsf{marg}} \rangle^{2}$ matrix, diagonal); $\mathbf{z}_{t}$ is $p \times 1$ z-score vector of trait $t$, or $\mathbf{z}_{t} = \boldsymbol{\theta}_{t}^{\textsf{marg}}/ \textsf{se}[\boldsymbol{\theta}_{t}^{\textsf{marg}}]$.

In basic zQTL model, spasrse parameter matrix, $\theta$ was modeled with spike-slab prior. We carry out posterior inference by variational inference with surrogate distribution first introduced in Carbonetto and Stephens (2012):

$$q(\theta|\alpha,\beta,\gamma) = \alpha \mathcal{N}\!\left(\beta,\gamma^{-1}\right)$$

We reparameterized $\alpha = \boldsymbol{\sigma}\!\left(\pi + \delta\right)$, and $\gamma = \gamma_{\textsf{max}}\boldsymbol{\sigma}\!\left(- \tau + \lambda \right)$ for numerical stability.

In factored zQTL model, we decompose sparse effect: $$\boldsymbol{\theta}_{t} = \boldsymbol{\theta}^{\textsf{left}} \boldsymbol{\theta}_{t}^{\textsf{right}}$$

Author

Yongjin Park, ypp@stat.ubc.ca, ypp.ubc@gmail.com

Examples


###########################
## A simple zQTL example ##
###########################

n = 500
p = 2000
m = 1

set.seed(1)

.rnorm <- function(a, b) matrix(rnorm(a * b), a, b)

X = .rnorm(n, p)
Y = matrix(0, n, m)
h2 = 0.25

c.snps = sample(p, 3)

theta = .rnorm(3, m) * sqrt(h2 / 3)

Y = X[, c.snps, drop=FALSE] %*% theta + .rnorm(n, m) * sqrt(1 - h2)

library(dplyr)
library(tidyr)

qtl.tab = calc.qtl.stat(X, Y)

xy.beta = qtl.tab %>%
    dplyr::select(x.col, y.col, beta) %>%
    tidyr::spread(key = y.col, value = beta) %>%
    (function(x) matrix(x[1:p, seq(2, m+1)], ncol = 1))

xy.se = qtl.tab %>%
    dplyr::select(x.col, y.col, se) %>%
    tidyr::spread(key = y.col, value = se) %>%
    (function(x) matrix(x[1:p, seq(2, m + 1)], ncol = 1))

out = fit.zqtl(xy.beta, xy.se, X,
                     vbiter = 3000,
                     gammax = 1e3,
                     pi = 0,
                     eigen.tol = 1e-2,
                     do.var.calc = TRUE,
                     scale.var = TRUE)

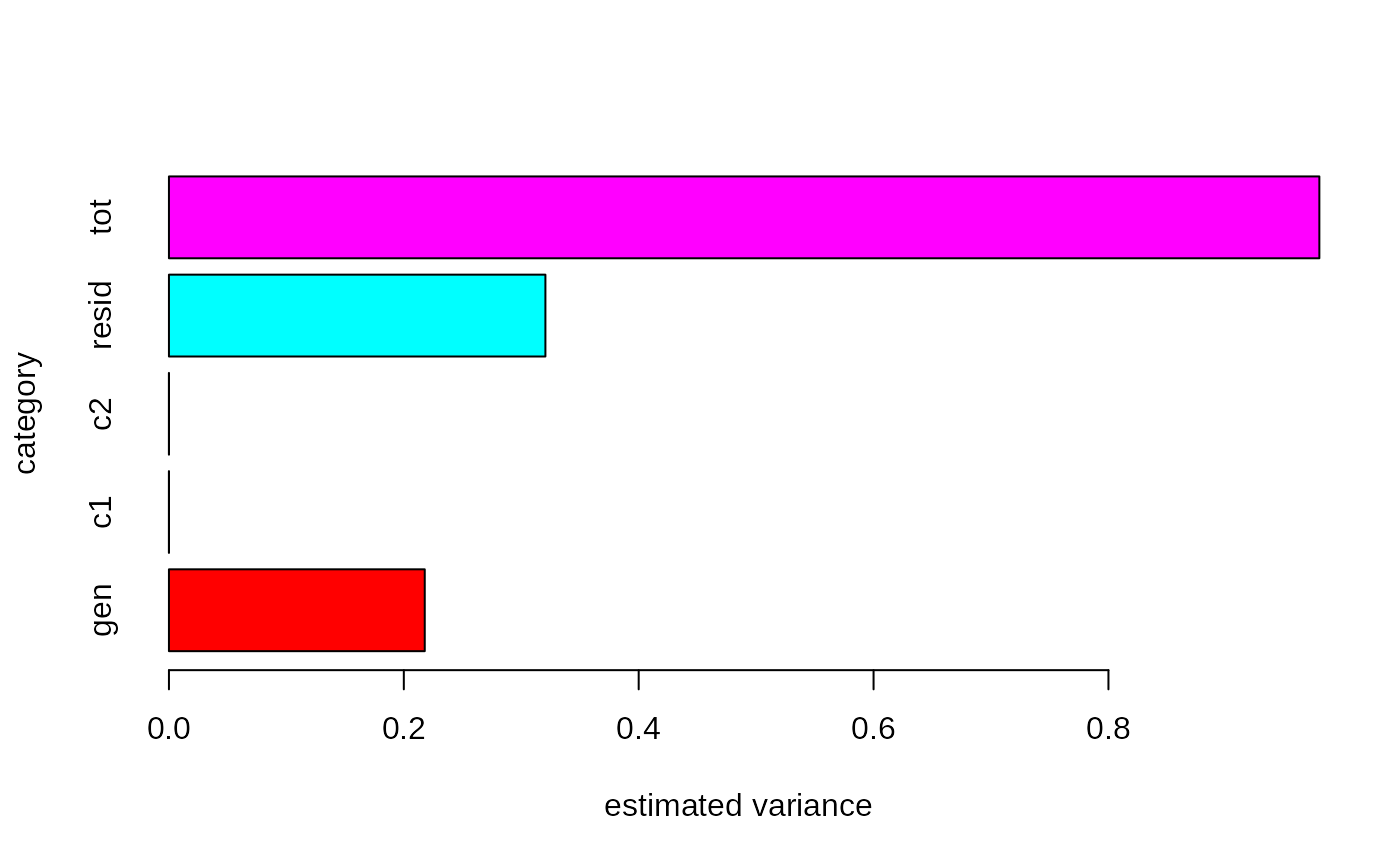
plot(out$param$lodds, main = 'association', pch = 19, cex = .5, col = 'gray', ylab = 'log-odds')
points(c.snps, out$param$lodds[c.snps], col = 'red', pch = 19)
legend('topright', legend = c('causal', 'others'), pch = 19, col = c('red','gray'))


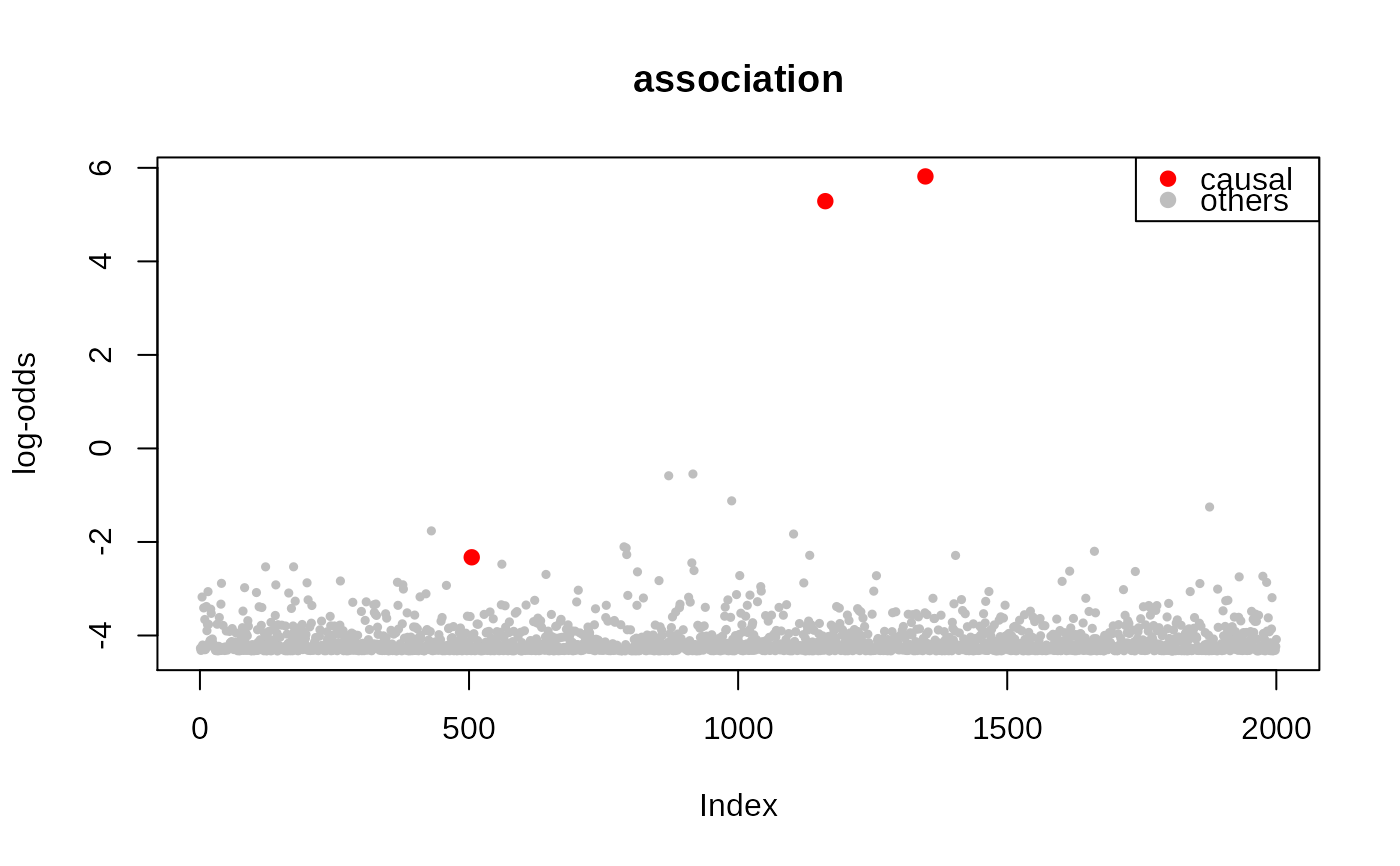.var = c(out$var$param$mean,
         out$var$conf.mult$mean,
         out$var$conf.uni$mean,
         out$var$resid$mean,
         out$var$tot)

barplot(height = 10^(.var),
        col = 2:6,
        names.arg = c('gen', 'c1', 'c2', 'resid', 'tot'),
        horiz = TRUE,
        ylab = 'category',
        xlab = 'estimated variance')