Table of Contents

We hear lots of excitement about a transformer network. However, I did not find an easy explanation (at least to me) on why and how it works.

1. How should we "embed" (locate) genes (words)? And why do we need embedding?

Embedding is like mapping a gene expression value in some latent space well spread between the values. In other words, from a point in the embedding space, we can recover each gene's name and its expression value (or ranking). It's important to understand what the embedding of a gene onto $d$-dimensional space does. Since my mindset has been stuck in a matrix factorization-like model for many years, I find this embedding step quite counter-intuitive. My other complaint is that "embedding" is not a good terminology at all. I think the whole step is more closely related to "stochastic" registration, dictionary, etc (just my complaint).

A document (or cell) as a bag of words

While not doing explicit embedding, in a typical fully connected neural network layer, we mark (or implicitly embed) a gene to a unique index (a variable or a visible unit). However, gene expression counts are not uniquely handled. In other words, the same gene can be "replicated" as if we keep on adding its contribution to the next hidden layer. The underlying concept seems very similar to Replicated Softmax: an Undirected Topic Model.

If we have a softmax model that maps for each word $d=1,\ldots,D$, we would have the energy function (to be minimized):

$$E = -\sum_{d=1}^{D} \sum_{g} \sum_{k} W_{gk}^{(d)} v_{g}^{(d)} h_{k}$$

where we denote $g$ for a gene $g$ and $k$ for a factor/topic $k$; $v_{g}^{(d)} = 1$ if and only if a gene $g$ is present in a document $d$; each word $d$'s model have weights $W_{gk}^{(d)}$ between a topic $k$ and gene $g$.

Assuming all the models share the same weights, namely $W_{gk}^{(d)}=W_{gk}, \forall d \in [D]$, and $x_{g}$ counts the frequency of a gene $g$ across all the words in this document, we can simplify:

$$E = -\sum_{g} \sum_{k} W_{gk} x_{g} h_{k}$$

This makes sense if we take each document as "a bag of words," where each gene is independently drawn within a document, conditioning on the topic proportion and latent topic membership of the word.

What have we missed with the bag-of-words assumption?

Since bag-of-words models have been so successful for many years and seem good enough for single-cell modelling, it is hard to justify why we would need a more sophisticated language model. So, this is not an exhaustive survey on what the bag-of-words missed:

1. Monotone contribution: We cannot map gene (word) counts in a non-linear fashion, meaning that a higher count of a gene $g$ will always have more weight on the same gene $g$ toward the next layer, i.e., $W_{gk}$ will increase for a particular $h_{k}$. In NLP, double or triple negation expressions are difficult to understand with a bag-of-words model. If a certain housekeeping gene (ribosomal or mitochondrial) is just highly expressed, its influence will dominate and mask out subtle yet significant context-dependent changes.

2. Lack of dependency within a layer: We need many layers to represent word-to-word non-linear relationships. A single layer of the softmax model cannot represent ordering or any sort of positional information across words. Using a softmax function or similar can have some effect of "lateral inhibition"-like mechanisms so that a sparse set of keywords can be selected for each topic. However, it can also make known or unknown stopwords appear across multiple topics without apparent meaning. There is no direct influence across topics that having some high-frequency word in one topic prevents the other topic from picking up the same words, except for some statistical pressure.

Gene embedding is like word embedding in NLP

An embedding can bring more flexibility on interpreting the number of the same word (gene) occurred within a document (cell). First of all, what is "word embedding?" In PyTorch's documentation for Embedding class, it says:

• Input: (*), IntTensor or LongTensor of arbitrary shape containing the indices to extract and
• Output: (*,H), where * is the input shape and H = embedding_dim

For scGPT, this embedding class is directly applied to integer-valued expression tensor.

In a nutshell, each cell is like a fixed length (number of words) document (or sentence). Discredited/binned gene expression levels on each gene (word) uniquely mapped onto some $d$-dimensional latent space. For instance, $x_{g}=1$ and $x_{g}=10$ are independently located in the embedding space. Upon training, we may be able to tell whether $x_{g}=1$ and $x_{g}=10$ mean semantically similar but very different from $x_{g}=5$. A gene embedding step clearly brings non-monotone expressivity in a language model. Anecdotally, "not" and "not, not, not" can be located in nearby locations apart from "not, not" if that's easier to picture. We do not specify their positions but learn semantic similarity from examples.

Some single-cell foundation models consider a positional embedding. Well, it can bring a gene-centric anchor point, but I personally don't think it could be redundant because each gene is uniquely mapped onto a specific position of a document. As long as we keep all the protein coding genes, more or less, I think positional encoding add little value to the frequency encoding.

2. What attention mechanisms can do with gene embedding vectors?

Now, let's discuss the elephant in the room: What in the world is attention? Why is attention all you need? First, we need to know what else has been considered so essential in previous work besides attention mechanisms. In NLP, a sentence of words has been modelled as a sequence of hidden states, such as recurrent neural network (RNN) models. One of the most recent RNN architectures is Long Short-Term Memory (LSTM), where the layer keeps the memory of previous words' hidden states to figure out the state of a current word. Since "memory" is not a part of the model parameters, it is somehow wasted, computationally cumbersome and not ideal for dealing with long sentences.

How can we represent a sentence of words in a meaningful way?

Okay. We need to model word-to-word dependency structures without inferring what each word's state could be. Why did we want to assign some latent states to words in a sentence? From the perspective of a hidden Markov model (a grandfather of a language model), knowing previous states, we can identify blocks of consecutive words, and then we can aggregate information within each block without too much loss of information. Keeping memory in the model is useful to parse out the meaning of a sentence. It might be an effective way to explain what the meaning of an overall sentence would be for a non-native English reader/writer, segmenting a sentence into multiple blocks (clauses), and so on. At the same time, such a pedagogy could become an obstacle when students want to generate a new sentence by themselves.

An attention mechanism simplifies this sentence-generating process.

It is like the way a baby learns a new language to me. A stream of words comes as a sentence. The first word will be understood together with other words that arrive later in the same sentence. It might be the imminent one or much later. As a neural model accumulates examples of sentences, associating the first word with others, the second with others, and so on, we can follow the probability of such word-to-word associations. Provided that the order of genes within a cell sentence/document is fixed, we can keep track of how frequently genes are jointly associated (or disassociated). For each gene, we can fit a softmax function (probability) to learn about frequent "neighbours" in the embedded space. Well, very roughly. For this type of process, there is no memory of word-specific states. In other words, if we consider a single cell as a scene of a movie or play, we don't need to know whether a gene plays an antagonist or protagonist in the scene. We just need to know who else appears here and how they interact with one another.

Hashing, dictionary, and (query, key, and value)

Interactions between genes matter, and keeping track of interactions is our only interest. For simplicity, although we don't need to do so, let's assume that gene embedding coordinates are fixed.

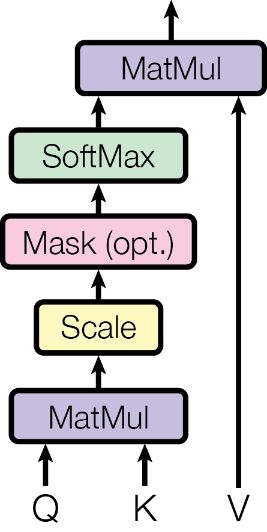
We need to bring two genes closer if they talk to each other more frequently than others. Borrowing the concept of locality sensitive hashing, we use a query of one gene to locate neighbouring genes according to their key in the embedding space. For closer gene pairs key and query should be similar, while distant pairs have largely independent key and query patterns. We could revise the embedding coordinates directly based on semantic similarity scores. However, if we want to stack up this gene-to-gene matching process within many different contexts, defining additional transformation functions for key and query vectors can render a more general modelling capability. More specifically, for the embedding vector of a gene $g_{1}$, namely $x_{g_{1}}$, and other $g_{2}$, namely $x_{g_{2}}$, we transform them into $[Q_{g_{1}1}, \ldots, Q_{g_{1}d}]$ and $[K_{g_{2}1},\ldots,K_{g_{2}d}]$, $d$-vectors. Then, we test how well the query and key vectors agree with each other by taking the dot product; this proximity information can be scaled and converted to a probably by the softmax transformation.

$$\textsf{Attention}(Q,K,V) = \underbrace{ \textsf{softmax}\left( \frac{QK^{\top}}{\sqrt{d}} \right) }_{\color{blue}\textsf{proximity between genes}} V.$$

The value vectors, $V$, map how each gene can work. Roughly, we may think of a traditional fully connected neural network layer as a diagonal attention matrix and only the V matrix. There, we encode gene expression patterns into some hidden codes. Putting them all together, in terms of the scene analogy, genes act on some value $V$ here, while interacting with their partners and influencing one another. In the next scene, we see the consolidated net effects of the entire scene. Sure, we may rule out some genes/actors in the current scene as they fit in the story. Moreover, instead of considering all pairwise interactions, we may restrict/focus on feasible interactions, potentially set by physical constraints, such as protein-protein interactions and cellular locations.

3. Can attention-based models be foundational for single-cell RNA-seq modelling?

I think gene embedding is a good idea. Well, I also like the way we represent gene-gene interactions as a stack of attention layers. But could we derive a foundational model? For a model to be foundational, well, what features, characteristics, or properties should a model possess and demonstrate? Very roughly... If we roughly consider each transformer layer modelled by attention networks as a scene or a set of rules for generating a scene, we may be able to run a realistic show with fifty of them stacked together, so is true with diffusion-based models. Well, is it foundational? We may need to define what the "foundation" model exactly means, though. I will leave all these sorts of questions for other posts.